研究テーマ
強相関電子系の磁性と超伝導
磁性や超伝導など物質の示す基本的性質の理解には、電子間の相互作用の効果を解明することが重要である。したがって、電子系を多体問題として扱うことが、物質の理論的研究である物性理論の本質をなしている。特に電子間の斥力の相互作用の影響が顕著に現れている重い電子系や高温超伝導などの強相関電子系は現在の物性理論の最重要テーマとなっている。現在研究室で手掛けているテーマには以下のようなものがある。
重い電子系のミクロな理論
(1)重い電子系の理論的研究は、1980年台の半ばに一つのピークを迎えた。スレーブボゾンの平均場理論、グッツヴィラー型の変分理論、1/N展開、フェルミ液体論などが相次いで登場し、重い準粒子の記述に一応の成功を収めた。しかし、重い電子の超伝導、量子揺らぎの顕著な磁気秩序などを議論するには、もう少し精密な理論が必要なことを誰しも感じていた。我々は、近藤格子模型や、周期的アンダーソン模型の種々の極限を調べ、また計算物理的手法も併用することによって一次元近藤格子模型の基底状態相図を決定し、各相の特徴も次第に明らかになってきた。一次元では三つの相がある。ハーフフィリングの所は、交換相互作用の大きさによらず励起にギャップがあるスピン液体相で、近藤絶縁体の一次元版になっている。弱結合領域からハーフフィリングの極限にかけては、常磁性金属相が広がっている。低密度極限から強結合極限にかけて金属強磁性相が広がっているのは予想外のことで、多体系の精妙さを感じさせるものである。
最近の発展としては、密度行列繰り込み群を用いた一次元近藤格子模型の研究がある。厳密対角化では10サイトが扱える最大のサイト数であるから、数十サイトまで容易に扱える密度行列繰り込み群は有力である。密度行列繰り込み群の本格的応用は、その性質があまり良く分かっていなかった常磁性金属相を対象とした。有限系の両端から誘起されるフリーデル振動の周期を調べることにより、一次元近藤格子模型のフェルミ面が、伝導電子と局在スピンを合わせた密度で決まっている大きなフェルミ面であることがはっきりした。また、この常磁性相のラッティンジャー液体としての性質も明らかになった。
密度行列繰り込み群で有限温度の性質を議論しようとするアイディアは、密度行列繰り込み群の開発当初からあったが、実用に耐え得るものとはなっていなかった。量子転送行列の最大固有値を密度行列繰り込み群によって求め、バルクの系の熱力学量を求める有限温度DMRGがスイスのWang氏と柴田氏(現在東京大学大学院総合文化研究科、当時当研究室)によってほぼ同時に完成した。さらに、有限温度DMRGでは動的相関関数を温度の関数として求めることができる。解析接続に、最大エントロピー法を用いることによって, 一次元近藤絶縁体のギャップが温度の低下とともに形成されていく様子をつぶさに調べることができた。これで、一次元量子多体系の動的相関関数の有限温度における計算手法が確立されたことになる。
(2)重い電子系の物質群の中で最近進展のあった話題としてYb4As3の磁場誘起ギャップがある。Yb4As3は、室温以上では立方晶であるが、室温以下で三方晶系に歪む。低温での比熱は温度に比例し、電気抵抗は T2 の振舞いを示す。ホール係数から見積もられる電子数を考えると、それらの温度係数は強く増強されていて、小数キャリアー系の重い電子系と呼ばれてきた。しかし、最近の研究によると、温度に比例する比熱は、室温以下で一次元的に整列したYb3+イオンの示す一次元ハイゼンベルグ系としての比熱であることが中性子非弾性散乱などの実験により明らかになってきた。磁場を掛けると励起にギャップが生じ、その原因はここ数年のなぞであった。最近我々と東工大押川、斯波両氏、都立大酒井氏達との共同研究によって、その機構が Dzyaloshinskii-Moriya 相互作用によるものであることが明らかになった。一連の研究によって、その有効ハミルトニアンのミクロな導出、およびその連続極限で得られる低エネルギーの有効場の理論であるサインゴルドン理論を用いた解析がなされ実験との良い一致を見た。また、この理論から導かれる帰結の実験的検証が精力的になされている。
(3)1次元近藤絶縁体中の近藤ホール
金属中の不純物状態の研究には長い歴史がある。不純物状態のクーロン斥力が強くなると磁気モーメントが発生すると考えられる。実際、ハートレーフォック近似の解はそのようになっているが、磁気モーメントが存在するという描像が成り立つのは高温で、温度を下げて行くにつれ、母体の伝導電子との相互作用によって磁気モーメントが縮小し絶対零度では一重項を作って非磁性状態になる。これが、良く知られた近藤効果である。
では、絶縁体中の不純物状態が磁気モーメントを形成する条件はどのようになるのであろうか?特に、強相関絶縁体中での磁気モーメントの形成条件とその特徴を調べることは興味深い。1次元近藤絶縁体中の不純物状態にたいして、その不純物レベルとクーロン相互作用の関数として、磁気モーメントの発生条件を調べた。この問題は、母体の近藤絶縁体から不純物サイトの局在スピンを除いた場合ということも出来、その見方をすれば、近藤絶縁体中の近藤ホールの問題である。
われわれは、この問題を1次元の場合について調べ、一般に金属中に比べて、磁気モーメントが発生しやすく、磁気モーメントは絶対零度まで安定に存在する。面白いことには、不純物サイトのクーロン相互作用が引力であっても磁気モーメントが存在する領域があることが分かった。
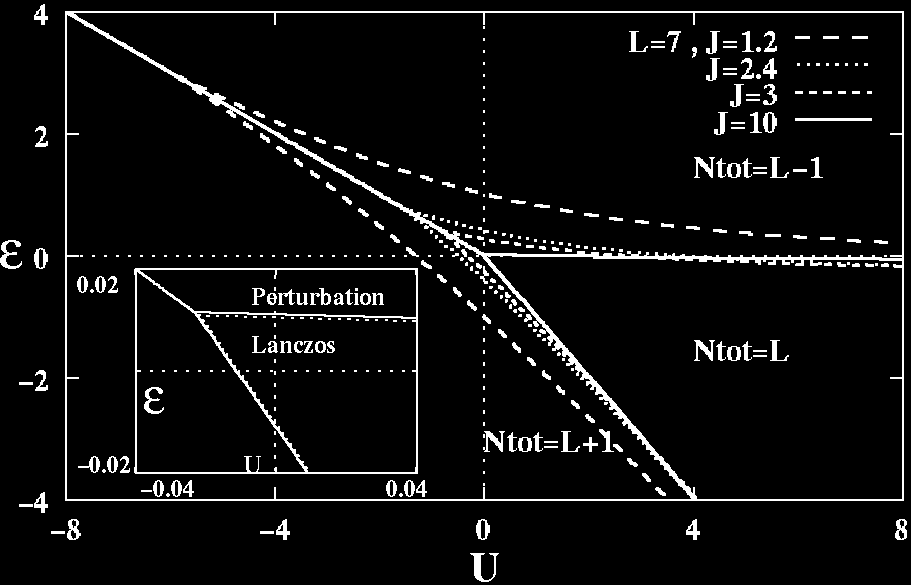
図.有限サイト数L=7での厳密対角化法による基底状態の相図。クーロン相互作用が引力(U<0)でも磁性状態(Ntot=L)が存在している。
(4)重い電子系の超伝導に対する軌道縮退の効果
最近重い電子系の研究が再び(三度?)活発になっている。そのきっかけを作ったのは次のような実験の進展である。
- CeIn3, CePd2Si2などで、 常圧下の反強磁性状態を圧力を掛けることによって抑制し、 反強磁性量子臨界点近傍で超伝導が実現された。
- UGe2, URhGeで、強磁性と共存する超伝導が発見された。
- CeTIn5(T=Ir, Rh, Co)の系で、新しい重い電子の超伝導が発見された。
重い電子系では、 f 電子の軌道縮退と伝導電子との混成に起因する複雑な電子状態のため、その超伝導に関する研究は、多くの場合、現象論的な範囲に留まって来たのが現状である。近年の物質合成の進歩は、ドハースファンアルフェン効果などの測定手段および相対論的バンド計算の進歩とあいまって、重い電子系に対しても多体効果をミクロな立場で議論できるに足る電子状態についての情報が得られるようになってきた。われわれは、実際の構造を反映した軌道縮退を考慮したモデルを構築し、その磁性と超伝導の研究をミクロな立場からすすめている。
フラストレーションの強いスピン系における量子相転移
(1)スピン系の量子相転移については、1998年から新たな対象の研究を推めている。当物性研究所上田寛研究室の陰山氏を中心とするグループがSrCu2(BO3)2という物質で、スピンギャップの存在と磁化プラトーを見つけたことが発端となった。この物質はCuBO3面が重要な役割を果たしている二次元的物質である。
我々はその研究を進める内に、その基底状態が約20年前ShastryとSutherlandが見い出した厳密なダイマー基底状態と同じものであることに気付いた。さらに驚くべきことには、SrCu2(BO3)2の三次元構造を考えても猶かつ、ダイマー状態が厳密な基底状態であることが明らかになった。この系の特徴はその励起状態にも現れ、トリプレット励起がほとんど局在し掛かっている。そのトリプレット励起の結晶化が磁化プラトーの原因と考えられ、磁化プラトーで磁気的超格子が形成される様子が明らかになってきた。
(2)フラストレーションのある量子スピン系は、量子揺らぎがフラストレーションによって増強されることが期待され、多くの研究者の関心を集めている。我々が研究を進めているSrCu2(BO3)2で実現されている直交ダイマー系(Shastry-Sutherland模型) も二次元における典型的なフラストレーションの強い系である。三次元では、パイロクロア格子(図1)やスピネル構造などが、フラストレーションの効果が重要な典型例として知られている。しかしながら、フラストレーションのある系では、(1) 負符合問題のため量子モンテカルロシミュレーションがあまり役に立たない、(2) 三次元系では有限サイズ効果の見積もりが事実上不可能なため厳密対角化などの手法も役に立たない、などの理由でその理論的研究は足踏み状態にあり、研究の新展開のためには何らかの新しいアイディアが必要と考えられる。
最近我々のグループでは、パイロクロア上のスピン 1 ハイゼンベルグモデルに対して、新しい描像を提案した。基本的なアイディアは、一次元の HaldaneGapの問題の物理的描像を与えるのに大きな役割を果たした Valence BondSolid の考え方を三次元パイロクロア格子に適用しようというものである。スピン 1 を二つのスピン 1/2 の合成と考えると、パイロクロア格子の基本単位である正四面体上のスピン 1/2 の系の基底状態はスピン一重項であるが、それは正四面体群の対称性を反映して二重に縮退している。この縮退を解く方法の一つとして格子との結合がある。これは一種の Jahn-Teller 効果であるが、格子歪みがスピン自由度とのみ結合している点でユニークで三次元におけるスピンパイエルス転移と見ることも出来る。その歪みの様子を図 2 に示した。ここに示した歪みは、ZnV2O4 や Mg2O4の構造相転移で実際に見い出されているものであり、これらの物質の構造相転移がここで提案した機構によるものである可能性が高い。
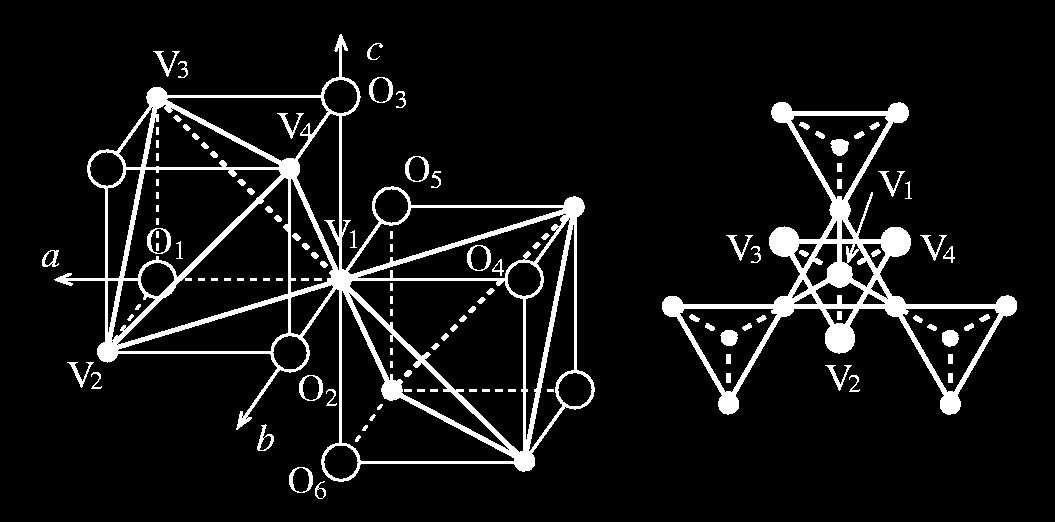
図1.ZnV2O4 の結晶構造(左図). 右図は[111] 方向から見たバナジウムサイトのネットワーク(パイロクロア格子)
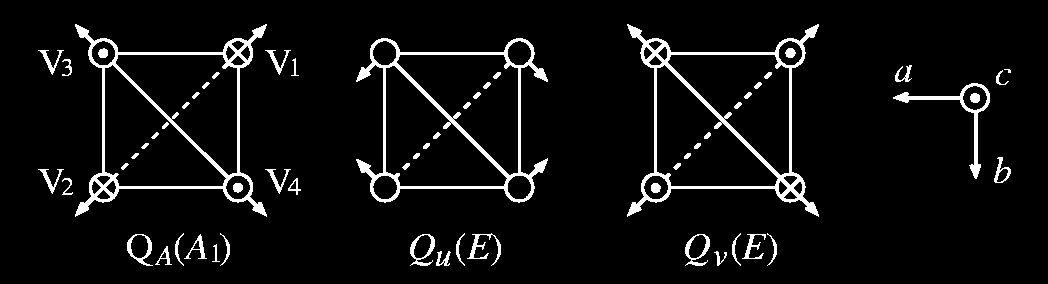
図2.正四面体の基準モード(A 表現と E 表現).全正四面体における一様なQv 格子変形が実験結果を説明.
高温超伝導の理論
高温超伝導の発見以来、その機構の解明が最大の問題であったが、秩序変数の位相に直接依存するπジャンクションを始めとする実験研究の結果、d波超伝導であることが確立した。このことは、一般的な意味でスピン揺らぎの効果がクーパー対形成の機構であることを意味している。実際、高温超伝導の正常相における一見「異常な」性質は、反強磁性量子臨界点に近い二次元金属と考えることによって理解することができる。残されていた問題は、低ドーピング領域における擬ギャップの問題と、ホール係数の問題である。
スピン揺らぎを扱う方法の一つとして、Fluctuation Exchange (FLEX)近似と呼ばれる方法がある。FLEX近似はBaym-Kadanoff流の定式化が可能であるから、帯磁率や伝導度などの二体相関関数に対しても保存則を満たす取り扱いをすることが、原理的には可能である。われわれは、電流の相関関数に対するバーッテックス補正を調べ、その中に反強磁性スピン揺らぎが発散する点で特異的な寄与を見い出した。このバーテックス補正の影響は、伝導度そのものに対してはフェルミ面上で平均され定量的な補正を与えるのみであるが、ホール係数では準粒子の運ぶ電流の方向依存性を直接反映するため特異的な寄与が強く現れ、ホール係数に顕著な温度依存性を生じることが明らかになった。この考え方では、温度に依存した寄与の符合がホールドーピングと電子ドーピングで異なることも自然に導かれる。
擬ギャップの問題は依然難しい問題として残されているが、ホール係数の定性的説明が可能となったことで、どう考えたら良いか見当がつかない物理量は、高温超伝導体の高ドーピング領域からアプローチする限り、なくなったと言えよう。
スピンと軌道の結合した系の量子臨界現象
最近、CeB6やLaMnO3系などいろいろな遷移金属化合物や、f電子系で軌道の自由度が顔を出し、スピンと軌道の結合した新しい量子効果の可能性が議論となっている。通常、軌道の自由度は格子変形と結合し、比較的高い温度で凍結してしまいがちであるが、その量子揺らぎが顕著な現象があるとすれば大変面白い。ハミルトニアンに交換相互作用型のスピンと軌道部分が積の形で入って、SU(4)対称性を持ったモデルは、その高い対称性のために量子揺らぎの特に顕著な系になっている。我々はこのモデルを一次元で調べ、その臨界的性質を研究した。このSU(4)対称な交換模型はベーテ可解で、漸近領域での臨界指数も共形場理論で求められているが、密度行列繰り込み群を用いて実空間の相関関数を求めた。さらに、このモデルのスピンに磁場を掛けていくと、SU(4)極限からスピンが完全に分極したSU(2)極限へとクロスオーバーしていくが、その様子も明らかにすることができた。
量子ドット系における輸送現象の理論的研究
近年、量子ドット系の近藤効果の研究が活発に進められている。典型的な量子ドットは、ゲート電極によるポテンシャルによって閉じ込められた微小な電子溜めに、電子を供給するためのソース・ドレイン電極が接続された構造となっている。そのために、量子ドットを用いた研究には従来の希薄磁性合金での近藤効果の研究にはない特徴がある。まず、ソース・ドレイン間に有限の電位差をかけ電流を流すと、定常的な非平衡状態が実現しているという点があげられる。さらには、ゲート電極のポテンシャルを変化させることによって、トンネル強度やドット内の電子数を変化させられるので、近藤効果に寄与するパラメータを任意に変えられるという点がある。
我々のグループでは、これらの側面から量子ドット系における輸送現象を理論的に研究している。
(1)非平衡状態にある量子ドット系における近藤効果
ソース・ドレイン間に有限の電位差をかけた際の近藤ピークに関して1つの未解決問題があった。アンダーソンモデルに対して平衡系ではきわめてよい近似であったクーロン相互作用の2次摂動の結果では、共鳴ピークが1つであるのに対し、noncrossing approximation (NCA) やその他の手法を用いた理論研究、さらには3つの電極をもつドット系を用いた実験では、左右のリード線のフェルミ準位の所に2つのピークが得られ互いに矛盾する結果となっていた。最近我々のグループでは、非平衡系を取り扱うKeldysh形式に基づき4次摂動までの計算を行い、近藤ピークは電位差が近藤温度より大きくなる時に2つに分離することを示した。
さらに興味深い点は、近藤ピークの分離が微分コンダクタンスに影響を与え、電位差が近藤温度より大きくなるとゼロバイアス以外に新しいピークが現れることを見出したことである。量子ポイントコンタクトにおいて近藤効果が生じていることを示唆する最近の実験において、微分コンダクタンスにおいて我々の得た結果と同じくゼロバイアス以外のピークが得られている。この結果をふまえ、この新しいピーク構造が量子ポイントコンタクトの0.7問題の理解にとって有用であるかもしれないという議論を行った。
(2) 近藤状態でのショットノイズ
メゾスコピック系での非平衡領域では、電荷が離散的になっていることから発生するショットノイズという量が現れる。この量の一番興味深い点は、単位電荷を決定できる可能性が示されていることであろう。実際に、ラフリン準粒子の分数電荷の観測に成功している。
こういった背景から、量子ドット系でもショットノイズの研究に焦点があてられてきた。低バイアス領域では、電流は近藤効果のユニタリティ極限からずれる。その反射カレントの有効的な電荷が見積もられ、普遍的な分数値5e/3が得られた。この普遍性に誘発される形で、実験や完全計数統計の文脈上の拡張など次々と報告された。そこで、くり込まれた摂動論を用いて、有効電荷は任意のク-ロン相互作用に対し、近藤効果のウィルソン比だけで決定されるという普遍的な特徴を明らかにした。この結果を軌道縮退がある場合にも拡張した。
(3) 有限温度密度行列繰り込み群を用いた量子ドット系の研究
ソース・ドレイン間の電位差をゼロとする極限では、量子ドットの輸送現象は平衡系として扱うことができる。この場合に、有限温度密度行列繰り込み群 (FT-DMRG) を適用することにより、量子ドット系に対する新しい計算手法を開発した。密度行列繰り込み群 (DMRG) は、一次元量子系に対して近年開発された強力な計算手法である 。 FT-DMRG はその多彩な発展の一部であり、量子転送行列に DMRG を適用することによって分配関数などの物理量を計算するものである。 FT-DMRG は、数値繰り込み群 (NRG) とは異なり比較的高温部分に限られるため低温領域を見るためにはパラメタをうまく選ぶ必要がある。このため、まず低温での帯磁率の逆数から見積もられる近藤温度を幅広いパラメタ領域に対して求めた。これは予想されていた概念的な相図を定量的に再現しするものとなっている。その知見に基づき、適切なパラメタ領域を選びコンダクタンスを求めると、高温領域でのクーロン振動から、低温領域でのユニタリティリミットまでのクロスオーバーを正しく記述することができた。FT-DMRG は量子転送行列法に基づいているため、様々なドット部分の転送行列に対して期待値を取るだけで物理量を一度に計算できるため、今後様々な量子ドット系に適用可能である。
メゾスコピック系の非平衡久保公式に基づくショットノイズ
メゾスコピック系は、マクロとミクロの世界をつなぐ中間的な領域にあることから、系の情報がランダム平均化を経ずに現れてくるという特徴をもっている。一般の非平衡領域では、電荷が離散的になっていることから発生する雑音:ショットノイズが重要になってくる。
(1) 非平衡久保公式とショットノイズ
最近、Keldysh 形式に基づき、微分コンダクタンスGの非平衡久保公式を導き、それが Sh=S-4kBG となることを示した。非自明な項としてカレント-電荷相関関数 Sh が 得られ、それを任意の温度でのショットノイズの新公式として提案した。理論的に計算された Sh は、実験の観測量である S と G から決定された S-4kBTG と比較検討できる。よって、非平衡久保公式に基づくショットノイズの新公式 Sh を用いた、任意の温度での新たな研究展開が可能となっている。
(2) 分数量子ホール系のエッジ状態のショットノイズと統計性
分数量子ホール効果の興味深い帰結の1つとして、分数電荷をもった
ラフリン準粒子の発見が挙げられる。単位電荷は電流から直接には観測できない。絶対零度で準粒子がエッジ間をトンネルする際のショットノイズから、分数電荷が決定できることが提案され観測にも成功している。ラフリン準粒子の特異性は分数電荷のみならず、フェルミ統計とボーズ統計の中間にある分数統計に従っている点にもある。絶対零度でのショットノイズからは電荷を決定できても、統計性の違いを観測することはできない。その後、分数統計を観測する方法がいくつか提案されたが、決定的なものはまだなかった。そこで、この有限温度のショットノイズを用いれば、統計性の違いを議論できることを提案した。
振動する磁性イオンの近藤効果
イオンが籠状構造を持つ物質群が注目を集めている。その籠状構造の中に他のイオンが内胞されていて、そのイオン半径が籠のサイズより小さいとすれば、内胞されているイオンは籠にぶつかるまでは比較的自由に動きうる。この状況は小児の玩具であるガラガラに似ているので、rattlingと呼ばれる。これは典型的な非線形振動子で、それ自体面白い問題であるが、今この内包されているイオンが磁性イオンであるとすると何が起こるであろうか。
こうした問題を考えるために、ポテンシャル中を振動する磁性イオンと伝導電子の系を記述する一般化されたアンダーソンモデルを構成した。局在軌道と伝導電子の混成項に対する振動の一次の影響を考える。このときフォノンの生成消滅には角運動量の変化が伴う。簡単のために、局在軌道が s 軌道であるとすると、通常の混成項は同じ対称性を持つ s 波の部分波とのみ混じりを生じるが、フォノンの出し入れを伴うと p 波との混成のチャンネルが新たに開くことになる。局在電子の電子間相互作用が強くて磁気モーメントが形成されている状況では、磁気モーメントの遮蔽は、どちらの混成項の方が強いかに応じて、s 波で遮蔽されたり p 波で遮蔽されたりする。二つのスクリーニングチャンネルが拮抗した時には2チャンネル近藤効果が実現する。下の図は、数値的繰りこみ群を用いて解析した固定点の違いによる基底状態相図である。